Metallurgical Considerations
Shell Forming Methods
Hand-Forming
The old-school, non mechanical way of making a shell for a steel sound sculpture is forming it blow by blow from a flat sheet of metal (manually or pneumatically). As the metal receives hammer blows with a force beyond the elastic limit (yield point) it deforms permanently, or plastically as metallurgists say. The ability of a crystalline material, such as steel, to plastically deform depends on the ability to dislocations in the crystal structure to move. Impeding the movement of dislocations will result in a strengthening of the material. Plastically deforming the metal with a hammer creates new dislocations and interlocks them. So, hand-hammering a sheet of metal in a shell for steel sound sculptures will work harden the material. The hardenability of the steel primarily depends on its carbon and manganese content. Also every plastic deformation will leave some (residual) stresses in the microstructure. All these effects have advantages: the hardening progressively increases the yield point which serves to create stable tone-fields. The tone-fields are staying in tune longer and do not deform by playing them. The residual stresses, especially the compressive stresses, are important for tuning. Without these stresses, the notes could not be made to vibrate at low frequencies. And finally, the dislocation density positively influences the damping characteristics, making the instrument sound louder.
A good steel for hand-sinking has to be ductile (soft) enough to be sinkable to an appropriate depth (so, low in carbon) and work-hardenable (but not ultra-low in carbon, as interstitial carbon helps to pin dislocations).
The disadvantages of hand-forming are the dependence on supplies of good material, the time to form a shell, potential health issues (Hand-Arm Vibration Syndrome) and the difficulty to form a shell with a regular thickness distribution (which complicates tuning and may degrade the sound; see below.).
Hydro-Forming
Water pressure can be harvested to “blow up” a shell from a clamped flat sheet of steel. It is a relatively straight-forward and easily replicable process. A hydro-forming machine for workshop use can be built for around 2500 – 4000 Euros (see here). As the hydro-formed shell is much less work-hardened compared to a hammer-formed shell, it needs to be hardened afterwards, e.g. with gas nitriding (see below). Hydro-forming is considerably faster than hammer-sinking, though. But like in hand-forming, the thickness distribution of the final shell is not equal. Typically the material will gradually thin out as one moves from the rim to top of the shell. The thinning can be controlled by adjusting the slipping of the sheet over the clamping rings during the forming process.
Drawing
In drawing, the shell is formed by an industrial press with a capacity of up to 400 tons. The tools for pressing the form are very expensive, but once done, the production is very fast and industrialized. Drawing is the only forming method which can produce shells with equal thickness distributions. Like in hydro-forming, the material has to be further hardened, though, to be usable for tuning (e.g. through gas nitriding; see below). Soma uses drawn shells from Shellopan and Ayasa.
Rolling/ Spinning
Yet another way of creating shells is by spinning the metal sheet and using a roller tool to mould it into its desired form and depth. While in spin forming the sheet is not clamped and rolled over a mandrel having the desired form, in rolling, the sheet is clamped and purely formed by the roller. The rolling process was patented by Pantheon Steel and recently released to the public. Rolling seems to be more beneficial to shell forming for handpans than spin forming as the thickness distribution can be better controlled and more stresses (dislocations) are added in the forming process.
Nitriding: Hardening and Stressing Shells
The most common process to harden hydro-formed or drawn shells is gas nitriding. It was introduced to singing steel by PanArt, the company which built the Hang ® . In the nitriding process atomic nitrogen is introduced in the surface layers of low-carbon steel. It is carried out in an ammonia atmosphere for periods of 4-120h (depending on depth of nitriding layer required) at temperatures of 500-580C. This process not only creates an efficient corrosive protection but it replicates the beneficial features of work hardening: introduction of compressive stress in the outer layer of the metal, hardening of the surface (due to the inhibition of dislocation motion as the atomic nitrogen is added) and lower (magnetomechanical) damping. Possibly the modulus of elasticity and, thus, the restoring force (see below) are also increased.
The advantage of gas-nitriding over pure work hardening lies in the controllability and repeatability of the process. Different sets of properties of the final shells can be explored by changing variables like nitriding time, temperature, atmospheric pressure, cooling time (elongates the nitride needles) and steel composition. The latter two variables have a strong influence on the amount of nitrides found in the material. Especially aluminium and titanium in the raw steel material are very powerful nitride formers and need to be controlled.
Stress-Relieving
Further hardening can be achieved by low tempering prior to and/or during the tuning process. The careful application of heat will redistribute and decrease residual (macro) stresses. On the one hand, this will increase tuning stability as regions of high stress concentrations, close to the yield point of plastic deformation, are relaxed. On the other hand, a low temperature anneal artificially “age hardens” the material. The stress removal leads to an acceleration of the migration of carbon and nitrogen (if nitrided) to pin dislocations, thus strengthening the material.
Other methods of relieving and redistribution stresses include hitting the tone-field very hard with a stick or hammering with much obliquity (“stretching” action).
Additional Comments on Thickness (Distribution)
The bending stiffness of a plate is dependent on the elastic modulus of the material, the poisson ratio of the material and, to a large degree, on the thickness of the plate. A thin plate will have a reduced restoring force (see below) compared to a thicker one. Hence, it will be less sound efficient (lower in sound amplitude; “thin” sounding) but with a longer sustain. The vibrations of a thin steel plate are said to me of “low impedance” as they are dampened easily if an object, like the hand, stays too long on the plate. More importantly, though, the use of too thin a source material can lead to metallic or even chaotic sounding handpans (especially when played fortissimo) as the membrane will more readily perform chaotic oscillation patterns. Great care has therefore to be taken to ensure that the material does not thin out too much in the sinking process.
Additional Comments on Damping
The different damping mechanisms on the instrument include: acoustic radiation, material damping (magnetomechanical; which turns vibratory energy into heat), transmission losses across the note boundary and mode conversions at folds, edges and stress concentrations (the acoustically more efficient transverse waves are converted into longitudinal waves). Acoustic radiation is maximised by minimising material damping and transmission losses.
Additional Comments on Stainless Steel
Stainless steel has become more and more fashionable among handpan builders as parts of the community are seeking longer sustained sounds of the individual tone-fields. While we think that this impedes a more percussive playing style that we personally prefer, the longer sounds can create a more meditative atmosphere (part of it, of course, is because stainless handpans have to be played slower to not “drown” in the long-lasting sounds). The reason the tone-fields ring out substantially longer vs. the classical nitrided low-carbon steel handpans lies in the decreased damping coefficient of stainless steel. This will also make a stainless steel handpan sound more “metallic” and less “ceramic” as more untuned higher frequencies are heard during play.
Preparations for Tuning
Domes and Note Orientation
Once the shells are made, sufficiently stressed and hardened, there are two preparatory steps to make before tuning can start. The first one is stamping or hammering the domes (or sometimes called “dimples”) into the center of what later will be a tone-field.
The dome architecture is well known from traditional gongs in Gamelan music. Gong-smiths in Java call the central dome or boss “ucheng”.
Handpans are usually tuned with at least three harmonic frequencies in a 1:2:3 relationship. So, for example on an A4 note (440Hz; fundamental frequency) a first partial is tuned to a A5 (880Hz; first harmonic frequency; octave) and a second one to a E5 (1320Hz; second harmonic frequency; compound fifth).
The dome’s primary function in a handpan is to stiffen the central part of the tone-field. A dome is a highly rigid structure used extensively in architecture and nature for stability purposes (try to squeeze an egg with your hand!). Moulding the central part of the tone-field into a stiff dome fortunately does not affect the fundamental frequency too much. The stiffening leads, however, together with the fact that a handpan is played with a very soft “stick” (the hand!) to an attenuation of the higher partials of the fundamental frequency. These higher partials, if too audible, can give steel a sharp and sometimes piercing or metallic sound, especially when played fortissimo. A dome arranges or spreads the main vibrational areas of the partials almost symmetrically around and in a distance from it, in a way that if the dome is struck, these partials are receiving a minimum of impact energy and are thus barely audible (see holographic images on page 5 and 6 in this document). Instead, the dome architecture leads the energy predominantly into the lower tuned frequencies. Furthermore, and more importantly, the very high, metallic sounding partials will be pushed higher in frequency due to the stiffening effect of the dome. This will make them decay in amplitude faster. Otherwise, they will create a ring sound similar to a bell.
Since the dome also decreases the quadratic non-linear coupling coefficient (see explanation below), the tuned harmonics above the fundamental frequency are also dampened to a certain degree. So, a hand-played, domed tone-field tends to keep the impact energy in the lower partials with an increased emphasis on the fundamental frequency relative to a dome-less tone-field. This emphasis on the lower frequencies compared to e.g. a steelpan note makes the signature handpan sound more mellow.
Furthermore, the dome, adding stiffness to the center of the tone-field and resisting tensile stresses, increases intonation and tuning stability. This means that a domed sound sculpture can withstand repeated hand impacts very well.
Note orientation can play an important part in sound quality too. Measurements by Morrison and Rossing indicate that the sound radiation of the fundamental and the octave on a Hang ® is most intense over the note area and towards the center of the instrument. The compound fifth radiates sound sideways (see images on pages 8 and 9 here). This has implications for the building process: a note whose compound fifth shares the same frequency with an adjacent note’s octave (e.g. adjacent G4’s and D5’s) can render the sound of both notes impure, creating an annoying beating effect. The note orientation of the note with the compound fifth (the G4) has to be adjusted for this effect to not take place.
Note orientation also plays a role in acoustic radiation coupling through the air medium (they are usually weak, though) and mechanically through the steel (due to transmission losses at the note boundary). To decrease the mechanical coupling effect, sympathetic notes can be “hidden” behind other notes.
Furthermore, depending on the location of the player relative to the tone-field, the sound will be heard differently (especially the compound fifth). If you add room modes and spherical harmonics (see below) to the equation, a tone-field, depending on orientation relative to the player and depending on the room size and handpan cavity size, can sound quite differently.
Internote Shaping
Once the domes are set and the approximate borders of the tone-field are marked, all the area between the tone-fields, the internote space, has to be stiffened. This stiffening effect will occur due to further work hardening of the hammered areas (see above) and due to an increase of curvature (adding bending stiffness). As vibrational transmission losses across the note boundary will decrease the energy that can be held back in the tone-field (a damping effect), reducing the sustain and loudness of the note, properly isolating, “blocking”, a tone-field is crucial. Blocking is dependent on the internote space being more stiff than the enclosed tone-field through a process called mechanical impedance mismatching. The stiffer, high impedance, internote area will not be easily set into vibratory motion by the less stiff, low impedance tone-field membrane. To stiffen the internote area, the material is curved and work-hardened more than the note area.
Blocking will never be perfect, however. On the one hand this will result in some degree of mechanical energy losses as the tone-field boundary is set into small vibrations, on the other hand this enables mechanical note-note interactions and couplings to take place across the instrument (as mentioned before, weaker couplings can obviously, also take place via acoustic radiation through the air medium).
Tuning Parameters
Note Geometry
In order to vibrate or oscillate, a membrane requires two basic properties: a stiffnening or springlike quality to provide a restoring force (energy) when displaced and inertia (mass), which causes the resulting motion to overshoot the equilibrium position (a higher restoring force will increase the sound amplitude, lower the sustain (“kick”) and increase the frequency; higher mass will have the opposite effect). A handpan tone-field membrane can thus be looked at as a spring. In its tuned state on a sound sculpture this spring is under high amounts of compressive pre-stress (yes, compressive not tensile stress as in a drum skin). This compressed spring stores potential energy which is force released when the hand strikes the tone-field. The potential energy of the spring is transferred into kinetic energy and back from kinetic energy into potential energy and so on until this ongoing vibratory movement looses all its power through energy loss effects (due to mechanical losses, damping, acoustic and heat radiation).
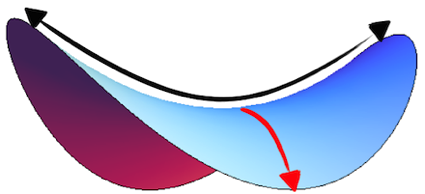
The force that is always directed back to the equilibrium position of the spring, opposing the displacement, is called restoring force. The strength of this force depends on the structural stiffness, which in turn is a function of pre-stress and shape of the tone-field and its boundary conditions. Since the dome adds stiffness to the tone-field (see above), compressive stresses along the note boundary have to be increased to reach the same (low) fundamental frequencies as without a dome. To increase the compressive (pre-)stress without the restoring force of the tone-field membrane going to zero (at which point the membrane reaches zero stability and buckles/flaps), a certain note geometry has proven favorable. A doubly-curved, or anticlastic, structure has one curvature axis under compression and the other one under tension (see picture below). Increasing the curvature in one direction leads to structural stiffness and strength in another direction. For example, whenever you hold a Pizza slice and curve the rim part to stiffen the slice to not sag (and spill the tomato sauce all over your shirt), you are employing this curvature strengthening effect. Anticlastic shapes are thus often used in architecture to couple the benefits of little material with high strength. In the tuning process, the tone-field membrane has to be stretched into an anticlastic shape. Simply deforming the membrane into this shape will not be possible, as it cannot be built from flat source material (if you don’t believe it try to wrap a piece of paper over a pringle chip without wrinkling the paper). What is important here is that the anticlasticity prevents the highly stressed membrane to perform chaotic movements, resulting in “wobbly” sounds (as it the oscillation pattern will not show a stable trough), or even collapse/ buckle under the increased stress load.
Tuning – Manipulation of Modes of Vibration
So what happens in the tuning process? It’s basically a hammer-induced manipulation process to get at least the three lowest modes of vibration to oscillate in a 1:2:3 frequency relationship. All three modes share the note boundary as a nodal line (area where the note membrane does not vibrate). The 2nd and 3rd mode of vibration each have an additional nodal line perpendicular to each other (the membrane, thus, vibrates at these modes with two halves of the tone-field in anti-phase motion). The hammer peening action around the note boundary sets the parameters for the elasticity of the membrane-spring and the compressive stress. Only areas of equal dynamic stiffness (in amplitude an direction) will define a note boundary. For steelpans it seems that a length/width ratio of the tone-field of 5-to-4 readily produces a 2nd mode and a 3rd mode of vibration in a 2:3 frequency relationship. Because of the dome architecture (see above) on a handpan this ratio can vary significantly between notes on the same instrument and among builders.
As handpan tone-fields are under compressive stress, the frequency of the fundamental will change with changes in compressive stress (more stress lowers the fundamental frequency). This is also the reason that the notes have a tendency to drift “sharp” (increase the frequency) as the stresses are relieved over time.
The higher modes of vibration, namely the 4h and 5th, especially on the lower notes such as the central tone-field (where these modes are not sufficiently stiff to be of a mere short duration), can also create audible tones. They are sometimes called “shoulder-tones” in handpan jargon. Their character is similar to a bell sound. As opposed to the 2nd and 3rd mode, they have one additional nodal line. To isolate them, a light tap with a pointy item at the end of the octave area (4th mode) and on the “corner” areas of the tone field (5th mode) will suffice. On a domed tone-field, their frequencies will usually fall somewhere around the third octave of the fundamental. At these high frequencies the sound usually decays fast if not excited directly at it’s vibrational “sweet spot” (as described above) or through parametric excitation or coupling effects (see below). They are usually very closely distributed in the sound spectrum (50-100cts apart), however. Tuning one of these modes to the third octave can significantly change the brightness of the overall sound of the note as mode coupling is enforced (see below).
Non-Linearity, Parametric Excitations and Quadratic Coupling
Many of the elements constituting a musical instrument behave approximately as linear systems. This means, that the acoustic output is a linear function of the mechanical input (e.g. the output of two simultaneously applied inputs is the sum of the two separate inputs). Steel sound sculptures, however, heavily depend on non-linear behaviour to create their distinct sound. The acoustic output is independent of the mechanical input. The most important non-linear parameter, the quadratic coupling coefficient, is directly proportional to the rise-to-thickness ratio of the tone-field (a flat plate would have a quadratic coupling parameter of zero).
A strong 1st (or fundamental) mode of vibration in a non-linear system will interact with itself (hence, the term “quadratic”) to create a so-calledparametric excitation, an audible sound, at exactly twice the frequency of the fundamental frequency. If the 2nd mode of vibration is tuned to twice the fundamental frequency, the parametric excitation of the 1st mode can (internally) resonate with the tuned 2nd mode. In this process energy is shifted from the 1st mode to the 2nd mode and back. This coupling effect is the strongest, producing a loud and resonant octave. If the 3rd mode is tuned to 3x the fundamental frequency there are more parametric excitations happening which can transfer energy from mode 1 and 2 to mode 3, from mode 2 and 3 back to mode 1, and from mode 1 and 3 to mode 2. There are also weak cubic couplings happening which transfer energy directly from mode 1 to 3 but they are not so relevant. Further parametric excitations are detectable at low levels at higher multiples of the fundamental (e.g. second octave at 4x the fundamental frequency, etc.). They can add an interesting flavor to the timbre (note: if the modes of vibration above the third mode are tuned to these weak parametric excitations – as in a steelpan – they will increase significantly in amplitude due to the internal resonance effect described above). In a domed tone-field, the higher modes of vibration are significantly dampened due to the stiffening effect (see discussion about the dome above) which means that there will be less energy transferred from the lower modes to these higher modes and thus more energy can be retained in the lower modes.
Coupling can also happen across the face of the handpan on two sympathetic notes (eg. G3 and G4). Pages 196 and 197 in Achong explain these energy exchanges verbally and graphically. On top of non-linear coupling effects, straight-forward linear effects will also take place (e.g. fundamental of G4 note excites octave of G3 note). On the downside, coupling between sympathetic notes slightly decrease the loudness of the fundamental and the octave as more energy is transferred.
Factors other than the rise-to-thickness ratio that influence the strength of the coupling are note shape, boundary conditions, blocking, hardening (nitriding) and annealing.
Modulations
When quadratic couplings are strong, deep amplitude and frequency modulations can occur and account for the distinctive tonal structure of the instrument. Without these modulations the sound of a handpan would feel synthetic, stale or even dead. The modulation dependence of a sound sculpture sound also makes it very difficult to record. Amplitude modulations (AM) are generally considered more important for a “good” sound than frequency modulations (FM). Other words often used for AM are “tremolo” and “vibrato” for FM, respectively.
AM’s on a handpan are perceived as resounding “wah-wah’s” which are created when the loundness of the tone oscillates as the energy shifts between modes.
In FM the frequency varies slightly during the course of the vibrating process. Scientists have found, for example, that FM’s are an important feature of a desirable human voice as it adds richness to its tone. The same seems to apply to sounds in general. If the FM’s on a handpan are too deep (too big of a pitch change), however, the sound could be perceived as warbling or wobbling.
Apart from increasing the coupling strength, these modulations are mainly adjusted by small detunings of the 2nd and 3rd mode frequencies relative to the fundamental frequency (more detuning slows the modulation rate). If the notes are tuned 100% correctly in a 1:2:3 relationship, there will be no modulations and the resulting sound will be dull.
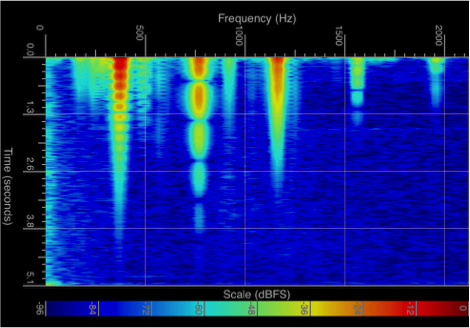
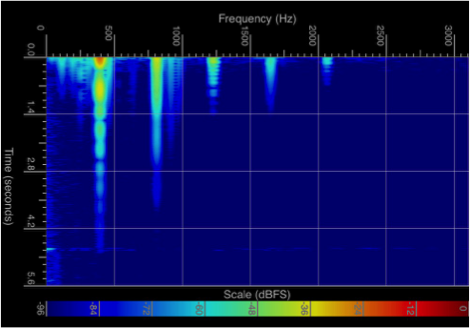
The following images show two spectrograms of the highest notes on two different Soma Sound Sculpture models (A4 and G#4). AM’s and FM’s are clearly visible due to strong quadratic coupling effects. Furthermore, one can see weak parametric excitations at higher multiples than the octave (x2) and the compound fifth (x3) at 4x and 5x the fundamental frequency (the amplitudes are weak as the higher modes other than the first three are usually not tuned harmonically on the higher notes and, thus, do not resonate with the parametric excitation).
Sound Radiation
As was already discussed above, note orientation has an effect on the direction of sound radiation. The efficiency of the sound radiation in general depends on the speed of the flexural waves of the vibrating note membrane. As the speed of the flexural waves approaches the speed of sound, the sound radiation efficiency increases markedly. The speed of sound depends mostly on temperature (lower at reduced temperatures). The speed of the flexural waves depends mostly on the thickness of the note membrane (positively related) and the frequency of the sound (positively related); further on Young’s modulus of elasticity of the material (positively related), the Poisson’s ratio of the material (positively related) and the density of the material (negatively related). Another source of increase in sound efficiency is the attached cavity (see explanation below).
Other Considerations
Effects of the Bottom Shell
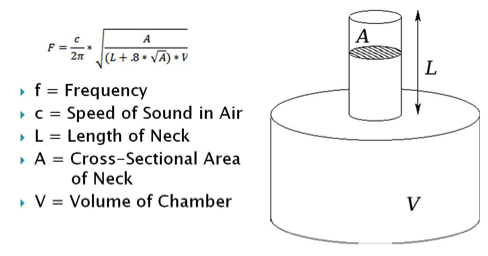
The enclosed air inside the handpan is responsible for some interesting effects. A positive sound effect is the Helmholtz resonance that the cavity produces. The hole on the bottom half, the “Gu”, acts as a neck to the sound chamber which forces the air, when excited, to act like a spring in the sense that the air is oscillating in and out of the chamber at a certain frequency. In accordance with the formula to calculate the Helmholtz frequency (see image below), closing the Gu hole will lower the cavity frequency. By putting the instrument on your lap and change your leg width, the effective size of the neck is increased and the Gu hole can be partially closed. This lowers the Helmholtz resonance frequency.
In a Soma Sound Sculpture the Helmholtz can be varied between roughly 60Hz and 85Hz. This sound can be heard in the background of every impact on the instrument. As the Helmholtz effect is not creating any harmonics (at multiples of the low Helmholtz frequency), it does not have a big resonating effect on the sound of the instrument (the resonance frequency is way lower than the lowest notes on a usual handpan). If a note was tuned low enough to resonate (linearily couple) with the Helmholtz frequency, the note has a very boomy, truncated sound absent of strong overtones which disturbs the overall sound of the instrument. For this reason, some “low” handpans with a very low frequency of the central tone-field have a closed Gu-hole.
The spectral peak of the Helmholtz resonance frequency, however, is quite broad, meaning that it does increase to a certain degree amplitudes of frequencies up to just about an octave above the resonance frequency. If the Helmholtz frequency is exactly one octave below the fundamental of the central tone-field, the “bass” sound increases a little (see here).
The cavity also helps to prevent to some degree the anti-phase sound waves emanating from the back of the note to interfere destructively with those of the front of the note which can cause cancellations and negatively alters the sound radiation efficiency (especially at lower frequencies). A good explanation of this effect and its importance can be found here.
Another positive effect of the attached bottom is to very tightly clamp the rim of the top shell, which would otherwise be more free to vibrate like a bell (as the rim is not a perfect node) and “draw” energy from the note vibrations. An unclamped rim will make the instrument unplayable. Even if just parts of the rim are not tightened enough, the reflected waves (transmitted across the note boundaries) will not be in anti-phase motion with the incident waves, resulting in an energy loss of the note close to the “lose” rim section. In the worst case scenario, the wave can drive the resonant frequency of the “lose” rim part and create an annoying, untuned sound. A more free rim in general converts the acoustically more efficient transverse waves into less efficient longitudinal waves which are predominantly audible as a ringing sounds.
The bottom shell also acts as a (passive) soundboard, thereby increasing the size of the wave propagating and sound radiating surface of the instrument. This is noticeable for the 2nd and 3rd modes of vibration which are much weaker radiators than the first mode of vibration (due to the anti-phase motion of the membrane in these two modes ; however, these modes have therefore longer decay times than the fundamental mode) . If a handpan is put on an inelastic surface, such as a stone floor, a noticeable damping effect (especially of the higher modes of vibration) can be perceived.
A clearly negative impact of the enclosed air are beating effects at certain frequencies. My best guess is that this phenomenon can be explained by the theory of spherical harmonics . As opposed to the air modes of the cavities of violins and guitars with their broad peaks acting as broad frequency range resonators, playing the handpan can create standing waves and echoes within the sphere. If these frequency peaks interfere with the sound waves of the tone-fields of similar but not identical frequency, an impure sound effect due to frequency beating will be created. Depending on the size of the cavity this “molesting” frequency can change. Spherical harmonics are the reason that on any size of the handpan, a certain frequency will not sound clean and will not be tuned in by most tuners. As the frequencies of these standing waves change linearly with cavity diameter, the “forbidden” note changes from A4 (56cm inner diameter instrument) to A#4 (53cm diameter) to B4 (50cm diameter) to C5 (47cm diameter). Other, higher spherical air modes, are also noticeable but are too high in frequency to efficiently disturb the performance of the instrument. You can test your handpan for resonant spherical harmonics by placing a speaker through the Gu hole and drive it with a tone-generator. Once you reach the first resonant frequency +/- 4 Hz (e.g. on a 53cm diameter Soma at around 465Hz) the sound will increase significantly in loudness. The only way to circumvent the problem of an impure sound at this standing-wave frequency is by placing the note (which has the fundamental frequency close to the disturbing frequency) much further away from the rim towards the top part of the instrument above the Gu-hole or by changing the length of the neck of the GU, i.e. with a cone-inset (this “Gu-cone” will just shift the “forbidden note” to another note, though).
Atmospheric Conditions
Temperature effects (especially exposure to direct sunlight) changes the thermal stress of the tone-fields. This has the same effect as increasing the compressive stress: the frequency of the note is lowered and the timbre changes (as the coupling parameters change with the change of the partial frequencies). This also affects the depth of modulations. Lower notes are more affected by thermal stress than higher notes. There is also a dampening effect on the sound when the temperature increases.
Furthermore, the temperature and the relative humidity of the playing environment affects the air density (weight of air). Both, temperature and humidity, are inversely related to air density. As the density increases, the vibrating note membranes gets more mass loaded by the surrounding air. If air is enclosed around the vibrating membrane (such as in an air cavity), there can be a slight rise in the fundamental frequency (and a drop in the upper harmonics) on lower notes, changing the coupling parameters. This effect gets more pronounced as the cavity and/or the opening of the cavity is tightened.
Lower temperatures can slightly increase the sound radiation efficiency as the speed of sound is decreased (see above).
Temperature also changes the properties of the (MS Polymer) glue bonding the two half shells together. These properties have an effect on the sustain of the notes and the timbre of the instrument. E.g. more glue will increase the absorption of the vibrations of the upper shell. As energy is lost in the process, the instrument sounds more damp in the higher partials and shorter in sustain. The glue’s elasticity, that is, the readiness for absorption, is slightly temperature dependent: as temperature increases, the elasticity is reduced and vice versa. All else equal, the glue will thus add to the sound a bit of dampening in cold temperatures and a bit of “openness” in warm temperatures.
Version 1.6 May 2020
September 2020
Panart AG recently started another attempt to claim copyright on the shape and design elements of the Hang® (see hcu.global for resources and background information). In these proceedings, Panart AG presented an expert opinion from Dr. Anthony Achong in German court. In collaboration other European handpan builders, we drafted an open letter addressing some of the claims made in the expert opinion.
Resources
- Anthony Achong, Secrets of the Steelpan
- Neville H. Fletcher & Thomas D. Rossing, The Physics of Musical Instruments
- Andrew Morrison & Thomas D. Rossing, The Accoustics of the Hang
- Ulf Kronman, Steelpan Tuning
- Uwe Hansen & Thomas D. Rossing, The Caribbean Steelpan, and some Offsprings
- Uwe Hansen & Thomas D. Rossing, Vibrational Mode Shapes in Caribbean Steelpans
- Felix Rohner & Sabina Schärer, Presentation @ Conference on New Developments of the Steelpan, Paris 2000
- Felix Rohner & Sabina Schärer, Hang – Blech Klang Skulptur
- Official Publications of Panart AG @ hangblog.org
- Jared Kearns, Hole Size in a Spherical Resonator